SENR/NRPy+: Simulating Colliding Black Holes on a Desktop

**Fig. 1:** A physically realistic simulation of the collision of two orbiting black holes, showing the evolution of `W` (one of 24 separately integrated fields in this particular formulation of general relativity). The specific meaning of `W` is not important here, except that its value drops to zero at the center of a black hole. This fact is used to track the locations of the black holes (green lines) as they orbit, lose energy by emitting gravitational waves, and merge to form a single black hole which finally settles down to an equilibrium state. The overall scale of the system is determined by the total mass `M`.

**Fig. 2:** Example validation test, measuring constraint violation along the radial direction on a spherical grid after evolving a black hole for a long time. The purple, green, blue, and orange curves show the result after using second-, fourth-, sixth-, and eighth-order finite differencing, respectively, holding the grid resolution fixed. This yields nearly exponential convergence of the constraint violation over large regions of the computational domain. The nonconvergent bumps near `r/M = 0` and `r/M = 400` are expected and well understood, and do not spoil the numerical simulation. See our publication for details.

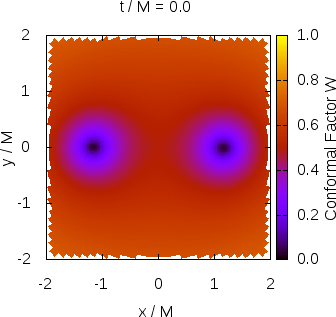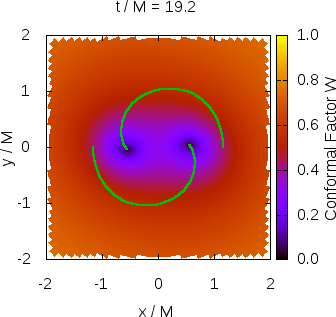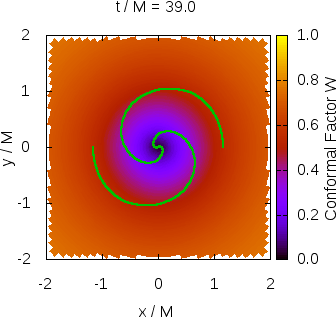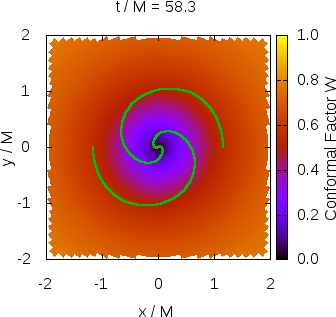
As gravitational wave detector technology improves instrument sensitivity for upcoming observation runs, the ripples in spacetime produced by the collisions of orbiting black hole binaries are detected at a rate of more than once per week. To accurately characterize the complicated waveform and extract useful physical information about the system from which it emanated, detailed calculations must be performed in the context of general relativity, spanning many orders of magnitude in time and space. The most widely used numerical relativity codes solve the equations of general relativity on computational grids with nested Cartesian boxes of varying resolution or intricate coordinate patches, both of which are algorithmically expensive and require high performance computing clusters in order to complete their calculations in a reasonable amount of time. Further, these methods induce a steep learning curve, limiting the contributions of new developers. This results in a throughput bottleneck from the theory side of multimessenger astronomy.

A new solution is here needed. Enter SENR/NRPy+!

I began development of the SENR/NRPy+ package in August 2016 with coauthor Zachariah B. Etienne. It has since grown into a powerful, efficient, fully functioning numerical relativity code, capable of producing physically accurate simulations of gravitational phenomena in general relativity, and beyond! Building SENR/NRPy+ was my primary research focus as a postdoctoral research associate at West Virginia University, where I applied my scientific training towards the theoretical understanding of gravitational wave sources. The code and its results are described in detail in our publication. I continue to contribute to this growing open-source project, located in the SENR/NRPy+ Git Repository.

SENR/NRPy+ is a new numerical relativity code, designed with efficiency in mind. By taking advantage of approximate symmetries in black hole binary configurations, it is possible to leverage massive savings in computer memory, up to ~180x fewer grid points than in Cartesian adaptive mesh refinement. This frees numerical relativity from the confines of the supercomputer, and opens the door to state-of-the-art science simulations on consumer-grade desktops (e.g., Fig. 1). When a new gravitational wave signal arrives, thousands of candidate runs can be launched simultaneously at the click of a button. The increased throughput results in greater opportunity for maximization of scientific insight.

As well as being efficient, the development philosophy strives for algorithmic simplicity. This makes it easy to implement new physics and coordinate system options, and friendly to new users.

Features

The SENR/NRPy+ code is an open-source, nonproprietary package for solving hyperbolic partial differential equations in singular, curvilinear coordinate systems. Adopting an orthonormal basis regularizes all tensor components. It is designed to be memory efficient, user-friendly, and easily extensible. The workflow is divided between two complementary parts, NRPy+ and SENR:

NRPy+

"Python-based code generation for numerical relativity and beyond"
Mathematical expressions written in Python in simple tensor-like notation
Cartesian-like, cylindrical-like, and spherical-like coordinate grids
Finite difference stencils of any accuracy order
Kreiss-Oliger dissipation
Common subexpression elimination optimization
SIMD vectorization enabled
Generate hyperbolic partial differential equation right-hand-sides and initial conditions, including Einstein's equations for general relativity, Maxwell's equations for electromagnetism, and the massless scalar wave field equations
Output highly efficient C code

SENR

"The simple, efficient numerical relativity code"
C code modules evaluate equations generated by NRPy+
Grid memory management
OpenMP parallelization
Runge-Kutta numerical integration
Automatic boundary conditions
Data storage checkpointing
Interfacing with the Einstein Toolkit

Combined, SENR/NRPy+ constitutes a fully functioning numerical relativity framework capable of generating precision 3+1 dimensional simulations of the orbital, merger, and ringdown phases of black hole binary evolution and the resulting gravitational wave signal.

Validation

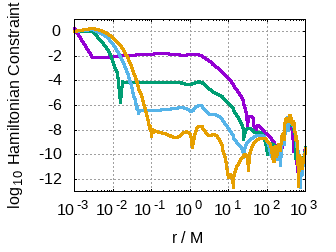
The SENR/NRPy+ code is extensively verified by comparisons with other established numerical relativity codes and by rigorous internal consistency and convergence tests. The equations of general relativity demand the constraint of certain evolved quantities. The violations of these constraints serve as measures of numerical error. In addition, known (highly symmetric) closed form solutions of the field equations are shown to behave exactly as desired within the context of the approximation, where truncation errors scale with resolution and accuracy order in precise agreement with the theoretical expectation (e.g., Fig. 2).